Precision Observations of Infant Supernova Explosions (POISE)

Shutter Test

How to take the shutter test (approx 20min):

i)   Put the telescope at the domeflats position.
ii)  Adjust the domeflat's lamp such you get 2000 counts in a 3 sec exposure.
iii) Take the following 5 exposures (object: shutter, exptype: flat) 

1) 1 exposure of 3 seconds
2) 1 exposure of 30 seconds
3) 1 exposure of 3 seconds
4) 1 exposure of 30 seconds, but pressing the pause button every 3 seconds.
5) 1 exposure of 3 seconds

And you are done!
If you have time, you can repeat the test replacing  3 by 4, 30 by 40,
and pressing pause in the 4th image every 4 seconds.

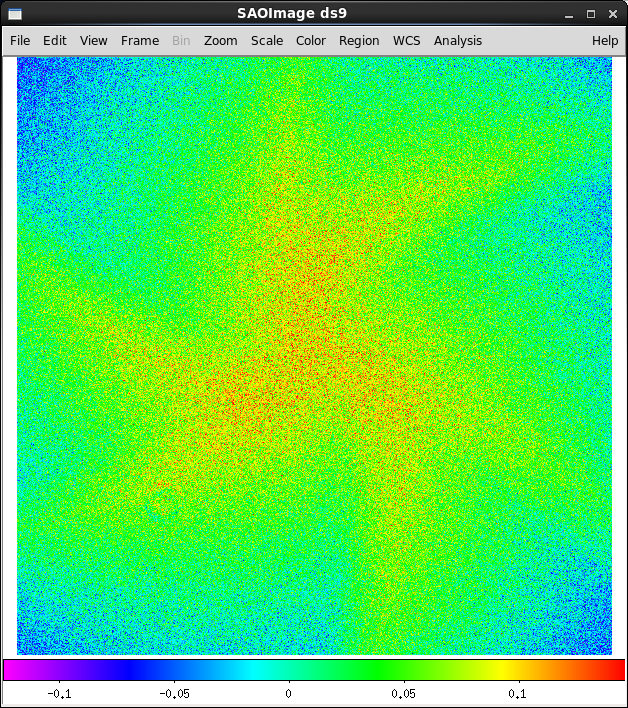
This is the resulting over-exposure whole detector pattern measured on Aug24th, 2014.

Linearity Test

How to take the linearity test (approx 1h30min):

1) Put the telescope at the domeflats position.
2) Adjust the domeflat's lamp such you get 2000 counts in a 3 sec exposure; set 'object' to 'linear'
and 'exptype' to 'flat'.
3) Run this macro taking the 4 quadrants simultaneously.

How to process the linearity test:

1) Copy the files into a csp machine.
2) Make a list of the images, one list for each quadrant.
For example:

	> ls ccd*fits | grep c1 > lt1
	> ls ccd*fits | grep c2 > lt2
	> ls ccd*fits | grep c3 > lt3
	> ls ccd*fits | grep c4 > lt4

3) Run the linearity test in the following way:

        > linear_test_swo_nc lt1  1 l1.txt 
        > linear_test_swo_nc lt2  2 l2.txt 
        > linear_test_swo_nc lt3  3 l3.txt 
        > linear_test_swo_nc lt4  4 l4.txt 

4) Send me the outputs (l?.txt files). Or, if you have a recent version of matplotlib in your pc/laptop
then you can run this python code there with the l?.txt files (csp machines 
have an old version unfortunately).

The result should something like this:

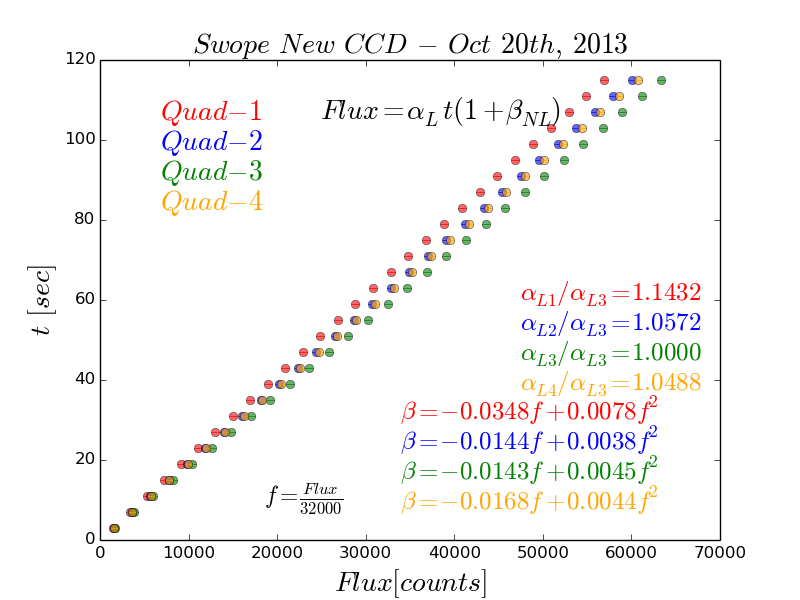
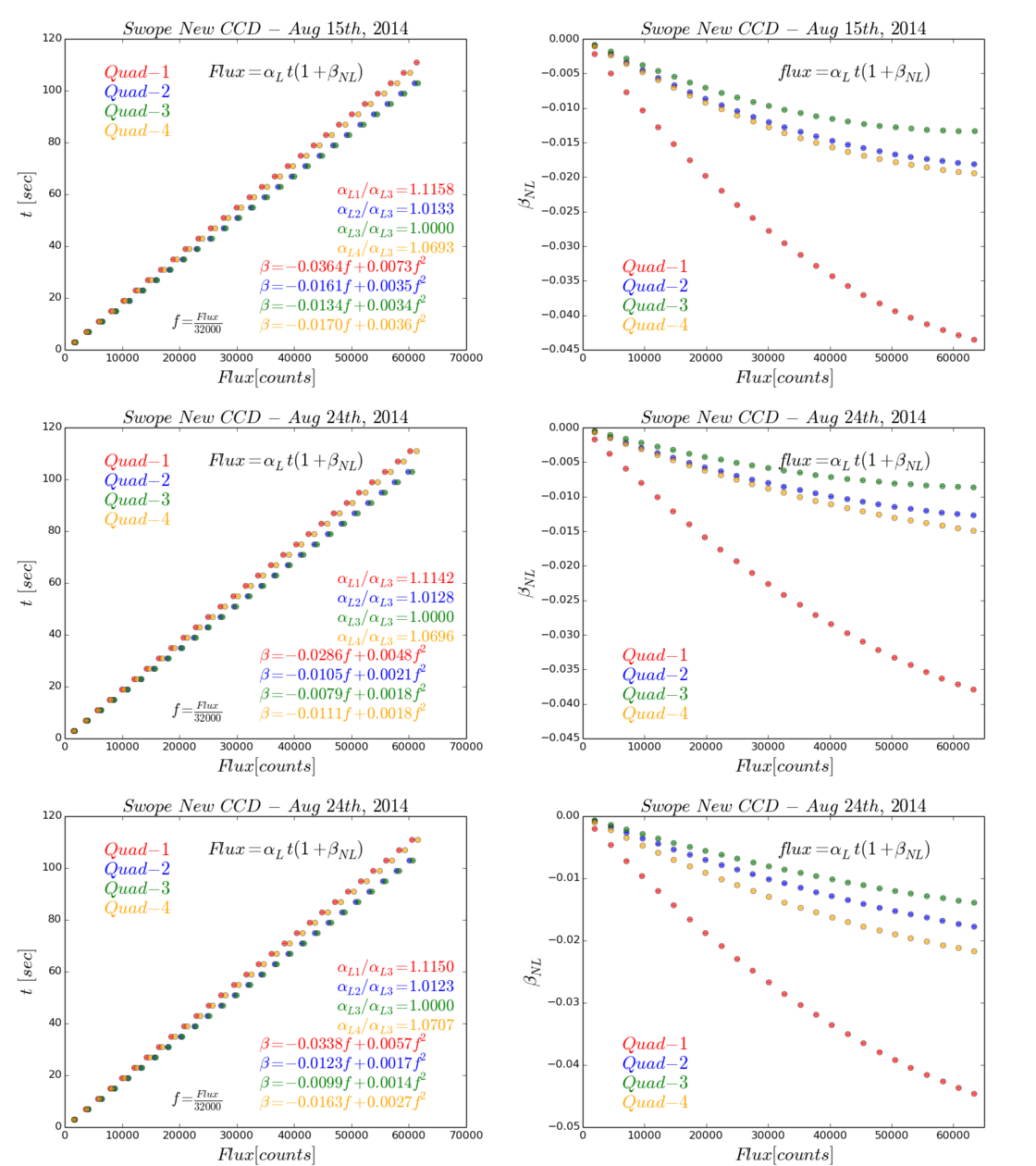
The following are linearity tests taken in Aug 2014, one in 15th and two in 24th.

The following is a linearity test taken in Oct 2014.

If you run the python code, check your numbers against the historical records:

Date Quadrant 1 --- α β(1) β(2) 2013 Oct 18 1.141 -0.035 0.0065 2013 Oct 19 1.140 -0.033 0.0063 2013 Oct 20 1.143 -0.035 0.0078 2013 Oct 21 1.146 -0.034 0.0064 2013 Oct 22 1.139 -0.035 0.0068 2014 August 1.115 -0.033 0.0057 2014 Oct 03 1.076 -0.036 0.0071	Date Quadrant 2 --- α β(1) β(2) 2013 Oct 18 1.059 -0.018 0.0040 2013 Oct 19 1.058 -0.017 0.0039 2013 Oct 20 1.057 -0.014 0.0038 2013 Oct 21 1.066 -0.020 0.0048 2013 Oct 22 1.050 -0.014 0.0027 2014 August 1.028 -0.012 0.0017 2014 Oct 03 1.008 -0.014 0.0028
Date Quadrant 3 --- α β(1) β(2) 2013 Oct 18 1.000 -0.017 0.0045 2013 Oct 19 1.000 -0.017 0.0048 2013 Oct 20 1.000 -0.014 0.0045 2013 Oct 21 1.000 -0.012 0.0027 2013 Oct 22 1.000 -0.012 0.0029 2014 August 1.000 -0.010 0.0014 2014 Oct 03 1.000 -0.011 0.0024	Date Quadrant 4 --- α β(1) β(2) 2013 Oct 18 1.051 -0.022 0.0054 2013 Oct 19 1.052 -0.023 0.0061 2013 Oct 20 1.049 -0.017 0.0044 2013 Oct 21 1.058 -0.027 0.0074 2013 Oct 22 1.056 -0.017 0.0035 2014 August 1.070 -0.015 0.0027 2014 Oct 03 1.038 -0.017 0.0034

Carlos